Calculando a Mediana com um Número Ímpar de Dados: Como Calcular A Mediana Quando For Impar Me De Exemplo
Como Calcular A Mediana Quando For Impar Me De Exemplo – A mediana é um conceito fundamental em estatística que representa o valor central de um conjunto de dados ordenado. Diferentemente da média aritmética (a soma de todos os valores dividida pelo número de valores), a mediana é menos sensível a valores extremos, ou outliers, que podem distorcer significativamente a média. Compreender a mediana é crucial para uma análise de dados mais robusta e precisa, fornecendo uma medida de tendência central mais representativa em situações com dados dispersos ou com valores atípicos.
O Conceito de Mediana em Estatística
A mediana é o valor que divide um conjunto de dados ordenado em duas metades iguais. Em outras palavras, 50% dos dados são menores ou iguais à mediana, e 50% são maiores ou iguais à mediana. Sua principal vantagem sobre a média é a sua resistência a outliers. Um único valor muito alto ou muito baixo pode afetar drasticamente a média, mas terá um impacto muito menor na mediana.
Diferença entre Mediana e Média

A média é calculada somando todos os valores e dividindo pelo número total de valores. A mediana, por sua vez, é o valor do meio em um conjunto de dados ordenado. A diferença crucial reside na sensibilidade a outliers. A média é fortemente influenciada por valores extremos, enquanto a mediana permanece relativamente estável. Por exemplo, em um conjunto de dados 1, 2, 3, 4, 100, a média seria 22, enquanto a mediana seria 3, refletindo melhor o centro dos dados.
Importância da Mediana na Análise de Dados, Como Calcular A Mediana Quando For Impar Me De Exemplo
A mediana é uma ferramenta valiosa para analisar dados, especialmente quando existem outliers ou quando a distribuição dos dados não é simétrica. Ela fornece uma medida de tendência central mais robusta e representativa em comparação com a média nesses cenários. Em situações como análise de salários, preços de imóveis, ou qualquer conjunto de dados suscetível a valores extremos, a mediana oferece uma perspectiva mais realista da situação.
Passos para Calcular a Mediana com Conjunto Ímpar de Dados
Calcular a mediana com um número ímpar de dados é um processo direto. Os passos a seguir demonstram como determinar o valor mediano.
- Organize os dados em ordem crescente: Arrume os números do menor para o maior.
- Identifique o elemento central: Com um número ímpar de dados, o elemento central é simplesmente o valor que fica exatamente no meio da sequência ordenada.
- Declare a mediana: Este elemento central é a mediana do conjunto de dados.
| Passo | Descrição | Exemplo (1, 3, 5, 7, 9) | Resultado |
|---|---|---|---|
| 1 | Organize os dados em ordem crescente | 1, 3, 5, 7, 9 | – |
| 2 | Identifique o elemento central | 1, 3, 5, 7, 9 | 5 |
| 3 | Declare a mediana | – | A mediana é 5 |
Exemplos Práticos de Cálculo da Mediana (Ímpar)
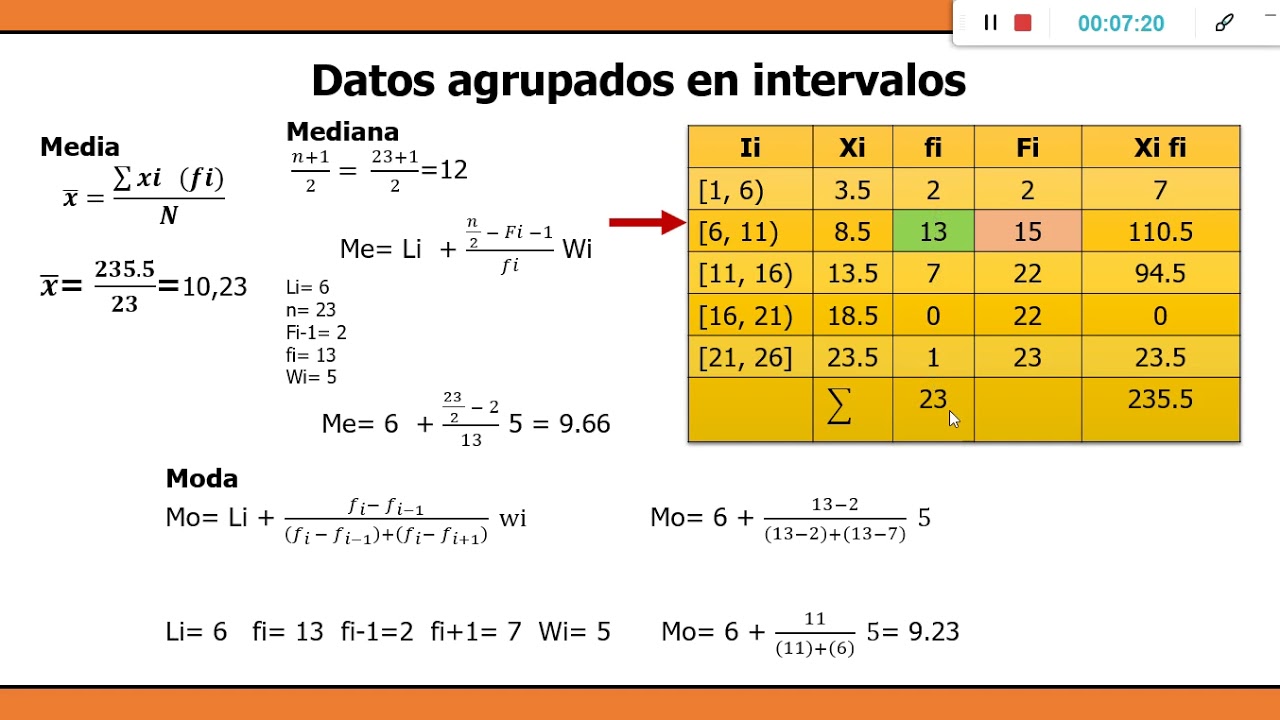
Vejamos alguns exemplos práticos para solidificar o entendimento do cálculo da mediana com um número ímpar de dados.
- Exemplo 1: 2, 4, 6, 8, 10. Ordenando os dados, temos 2, 4, 6, 8, 10. A mediana é 6.
- Exemplo 2: 15, 20, 25, 30, 35. Ordenando os dados, temos 15, 20, 25, 30, 35. A mediana é 25.
- Exemplo 3: 1, 5, 12, 18, 22. Ordenando os dados, temos 1, 5, 12, 18, 22. A mediana é 12.
| Exemplo | Dados | Dados Ordenados | Mediana |
|---|---|---|---|
| 1 | 2, 4, 6, 8, 10 | 2, 4, 6, 8, 10 | 6 |
| 2 | 15, 20, 25, 30, 35 | 15, 20, 25, 30, 35 | 25 |
| 3 | 1, 5, 12, 18, 22 | 1, 5, 12, 18, 22 | 12 |
Comparação entre Métodos de Cálculo da Mediana (Ímpar)
O método descrito acima é o método mais comum e direto para calcular a mediana com um número ímpar de dados. Não existem métodos alternativos significativamente diferentes para este caso específico. A simplicidade e a clareza deste método o tornam o preferido na maioria das aplicações.
- Método Direto: Simples, eficiente e fácil de entender. Vantagens: facilidade de cálculo; desvantagens: aplica-se apenas a conjuntos de dados com um número ímpar de elementos.
Aplicações da Mediana em Cenários Reais
- Salários: A mediana salarial é frequentemente usada para representar o salário típico de uma população, pois é menos sensível a salários extremamente altos ou baixos que podem distorcer a média.
- Preços de imóveis: A mediana do preço de imóveis em uma determinada região fornece uma medida mais representativa do preço típico de uma casa do que a média, pois é menos afetada por casas de luxo extremamente caras.
- Resultados de testes: Em avaliações de desempenho, a mediana pode ser mais informativa do que a média, especialmente se houver alguns resultados excepcionalmente altos ou baixos.
Ilustração Gráfica do Conceito da Mediana (Ímpar)
Imagine um histograma representando a distribuição de um conjunto de dados com um número ímpar de elementos. A mediana seria representada pela linha vertical que divide a área sob a curva do histograma exatamente ao meio. Em um gráfico de dispersão, ordenado, a mediana seria simplesmente o ponto de dados que está exatamente no meio da sequência. A representação gráfica facilita a visualização da posição da mediana em relação aos outros valores do conjunto de dados, tornando o conceito mais intuitivo e fácil de compreender.
Em resumo, calcular a mediana em conjuntos de dados ímpares é um processo relativamente simples, mas com implicações significativas na análise de dados. Compreender esse cálculo permite uma interpretação mais precisa e robusta de informações, evitando distorções causadas por valores atípicos. A capacidade de identificar a mediana, através da organização dos dados e localização do elemento central, torna-se uma habilidade essencial para qualquer profissional que lida com análise de dados, seja em pesquisas acadêmicas, estudos de mercado ou tomada de decisões em negócios.
Dominar esse conceito é fundamental para uma análise estatística eficaz e confiável.

