Múltiplos de Números Naturais: Conceitos e Aplicações: De Exemplo De Um Enunciado Envolvendo Multiplos De Numeros Naturais
De Exemplo De Um Enunciado Envolvendo Multiplos De Numeros Naturais – Este artigo explora o conceito de múltiplos de números naturais, desde sua definição básica até aplicações em problemas complexos e situações cotidianas. A compreensão dos múltiplos é fundamental para diversas áreas da matemática e para a resolução de problemas práticos em diversos contextos.
Conceito de Múltiplos de Números Naturais
Um múltiplo de um número natural é o resultado da multiplicação desse número por qualquer outro número natural. Por exemplo, os múltiplos de 3 são 3 (3 x 1), 6 (3 x 2), 9 (3 x 3), 12 (3 x 4), e assim por diante. A sequência de múltiplos de um número continua infinitamente. A relação entre múltiplos e a tabuada de multiplicação é direta: a tabuada de um número apresenta seus múltiplos.
Em uma reta numérica, os múltiplos de um número são representados por pontos igualmente espaçados, começando no próprio número.
| Múltiplos de 2 | Múltiplos de 3 | Múltiplos de 5 | Múltiplos de 7 |
|---|---|---|---|
| 2 | 3 | 5 | 7 |
| 4 | 6 | 10 | 14 |
| 6 | 9 | 15 | 21 |
| 8 | 12 | 20 | 28 |
| 10 | 15 | 25 | 35 |
| 12 | 18 | 30 | 42 |
| 14 | 21 | 35 | 49 |
| 16 | 24 | 40 | 56 |
| 18 | 27 | 45 | 63 |
| 20 | 30 | 50 | 70 |
Enunciados com Múltiplos: Problemas Simples, De Exemplo De Um Enunciado Envolvendo Multiplos De Numeros Naturais
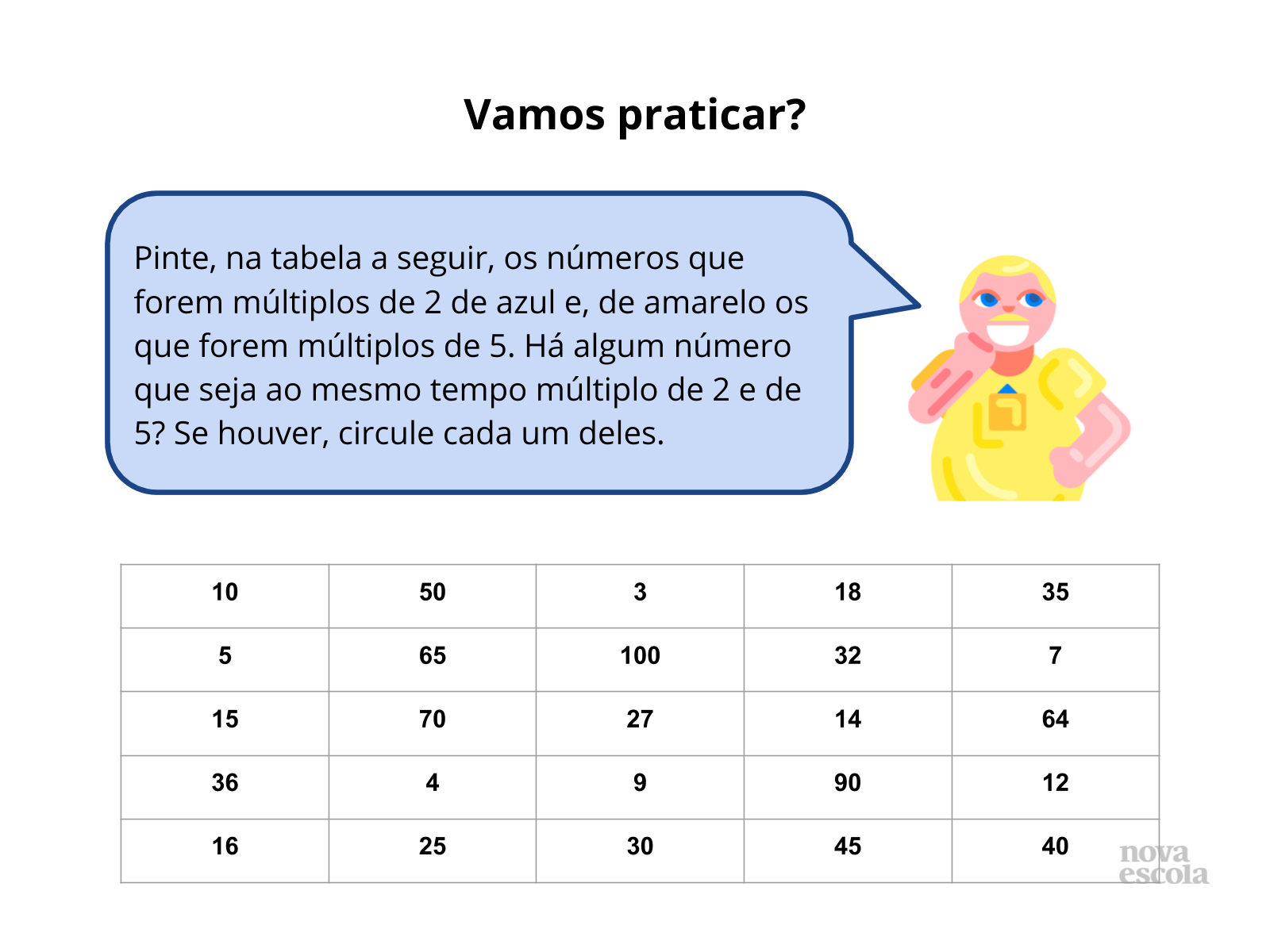
Problemas envolvendo múltiplos podem variar em complexidade. Problemas simples focam na identificação direta de múltiplos ou na determinação do menor múltiplo comum (MMC).
- Identificação de múltiplos: “Quais são os cinco primeiros múltiplos de 8?” A resposta envolve a simples multiplicação de 8 por 1, 2, 3, 4 e 5, resultando em 8, 16, 24, 32 e 40.
- Determinação do MMC: “Uma loja de doces vende bombons em caixas de 6 e 8 unidades. Qual o menor número de bombons que a loja deve ter para vender caixas completas de ambos os tipos?” Este problema requer o cálculo do MMC de 6 e 8, que é 24.
- Problema de contagem: “Maria está organizando seus livros em pilhas de 5 livros cada. Se ela tem 35 livros, quantas pilhas ela conseguirá formar?” A solução envolve dividir o número total de livros (35) pelo número de livros por pilha (5), resultando em 7 pilhas.
- Maior múltiplo em um intervalo: “Qual o maior múltiplo de 7 menor que 50?” Neste caso, a solução envolve dividir 50 por 7 (7 x 7 = 49), sendo 49 o maior múltiplo de 7 menor que 50.
Enunciados com Múltiplos: Problemas Complexos
Problemas mais complexos combinam múltiplos com outras operações aritméticas ou envolvem múltiplos comuns a mais de um número.
- Múltiplos e outras operações: “João tem 24 maçãs e quer dividi-las igualmente entre seus amigos. Se ele quer que cada amigo receba um número de maçãs que seja múltiplo de 3, de quantas maneiras ele pode distribuir as maçãs?”
- Múltiplos comuns: “Dois ônibus partem de um terminal simultaneamente. Um ônibus parte a cada 15 minutos e o outro a cada 20 minutos. Em quantos minutos os dois ônibus partirão juntos novamente?” Este problema requer o cálculo do MMC de 15 e 20.
- Múltiplos em geometria: “Um terreno retangular tem área de 48 m². Se o comprimento é múltiplo de 4 e a largura é múltiplo de 3, quais as possíveis dimensões do terreno?”
- Múltiplos versus divisores: Enquanto múltiplos são resultados da multiplicação, divisores são números que dividem um número sem deixar resto. A relação entre eles é inversa: se ‘a’ é múltiplo de ‘b’, então ‘b’ é divisor de ‘a’.
Aplicações de Múltiplos em Contextos Reais
O conceito de múltiplos está presente em diversas situações do dia a dia, facilitando a organização e a resolução de problemas práticos.
- Organização de objetos: Arrumar objetos em filas ou colunas iguais.
- Horários de ônibus: Prever o tempo de espera até a próxima partida de um ônibus que passa a cada determinado intervalo de tempo.
- Modelagem de situações com tempo ou medida: Calcular a quantidade de material necessário para um projeto de construção, considerando medidas múltiplas de uma unidade básica.
- Música: A organização rítmica em música frequentemente utiliza múltiplos para definir compassos e padrões.
Representação Visual de Múltiplos
A visualização de múltiplos auxilia na compreensão de seus conceitos e relações.
- Diagramas de Venn: Para múltiplos comuns, os conjuntos de múltiplos podem ser representados por círculos sobrepostos, com a interseção mostrando os múltiplos comuns.
- Diagrama de múltiplos comuns: Um diagrama que ilustra graficamente a interseção dos múltiplos de dois ou mais números, destacando os múltiplos comuns.
- Espiral de múltiplos: Uma espiral que visualmente representa os múltiplos de um número, mostrando seu crescimento progressivo.
- Relação múltiplos e divisores: Um diagrama que mostra a relação inversa entre múltiplos e divisores, utilizando setas para conectar os números.
Como encontrar o mínimo múltiplo comum (MMC) de dois números?
Existem alguns métodos, como a fatoração em números primos ou o método da listagem dos múltiplos. O mais eficiente depende dos números envolvidos.
Qual a diferença entre múltiplos e divisores?
Múltiplos são resultados da multiplicação de um número por outros números naturais. Divisores são números que dividem exatamente um número sem deixar resto.
Os múltiplos de um número são infinitos?
Sim, todo número natural possui uma infinidade de múltiplos.

