Exemplos De Planificação De Um Poliedro representam um tópico fundamental na geometria, explorando a relação entre formas tridimensionais e suas representações bidimensionais. A planificação de um poliedro consiste em desdobrar suas faces para formar um padrão plano, que pode ser usado para construir o poliedro original.
Este processo permite uma compreensão mais profunda da estrutura e das propriedades dos poliedros, além de oferecer aplicações práticas em áreas como arquitetura, engenharia e design.
Este artigo apresenta uma análise detalhada dos diferentes tipos de poliedros, com foco em suas características distintivas e na aplicação de métodos de planificação. Através de exemplos práticos e diagramas, o leitor poderá visualizar o processo de planificação e compreender como ele pode ser utilizado para criar objetos tridimensionais a partir de planos bidimensionais.
A discussão abrange também a aplicação da planificação de poliedros em diferentes áreas, explorando suas aplicações em projetos de embalagens, estruturas e obras de arte.
Tipos de Poliedros
Um poliedro é um sólido geométrico tridimensional que é limitado por um número finito de faces planas. As faces são polígonos e as arestas são os segmentos de reta que formam os lados das faces. Os vértices são os pontos onde as arestas se intersectam.
Existem diferentes tipos de poliedros, cada um com suas características únicas.
Poliedros Convexos e Não Convexos
Um poliedro convexo é um poliedro em que qualquer segmento de reta que conecta dois pontos dentro do poliedro está totalmente contido no interior do poliedro. Um poliedro não convexo é um poliedro que não é convexo.
Prismas
Um prisma é um poliedro que possui duas faces paralelas e congruentes chamadas bases, e faces laterais que são paralelogramos. As bases podem ser qualquer polígono.
O número de faces laterais de um prisma é igual ao número de lados da base.
- Prisma triangular: possui bases triangulares e três faces laterais.
- Prisma quadrangular: possui bases quadradas e quatro faces laterais.
- Prisma pentagonal: possui bases pentagonais e cinco faces laterais.
Pirâmides
Uma pirâmide é um poliedro que possui uma base poligonal e faces laterais que são triângulos que se encontram em um ponto chamado ápice.
O número de faces laterais de uma pirâmide é igual ao número de lados da base.
- Pirâmide triangular: possui base triangular e três faces laterais.
- Pirâmide quadrangular: possui base quadrada e quatro faces laterais.
- Pirâmide pentagonal: possui base pentagonal e cinco faces laterais.
Sólidos Platônicos
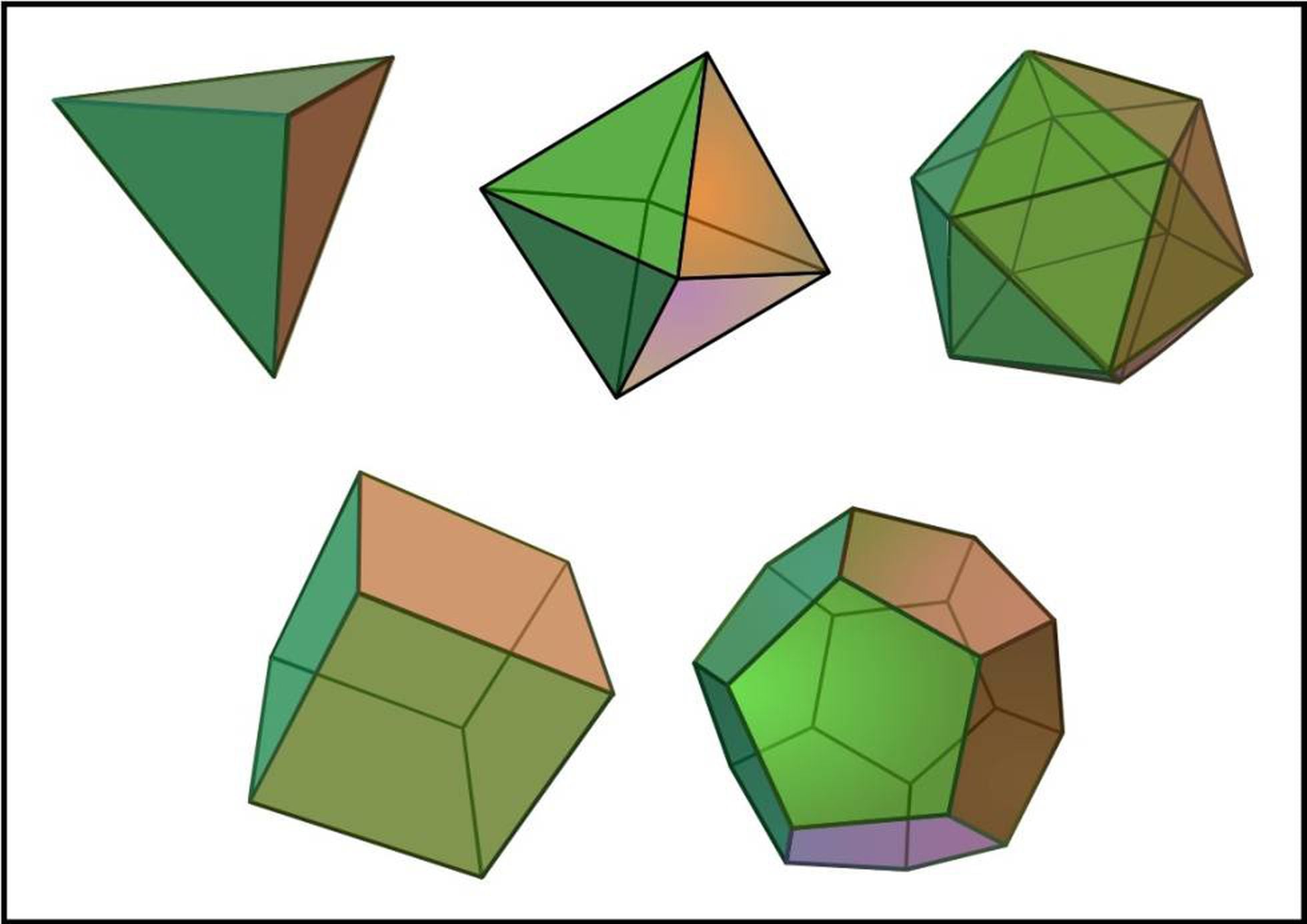
Os sólidos platônicos são poliedros convexos regulares, ou seja, todos os seus lados são iguais e todos os seus ângulos são iguais. Existem cinco sólidos platônicos:
- Tetraedro: possui quatro faces triangulares, quatro vértices e seis arestas.
- Cubo: possui seis faces quadradas, oito vértices e doze arestas.
- Octaedro: possui oito faces triangulares, seis vértices e doze arestas.
- Dodecaedro: possui doze faces pentagonais, vinte vértices e trinta arestas.
- Icosaedro: possui vinte faces triangulares, doze vértices e trinta arestas.
Sólidos de Arquimedes
Os sólidos de Arquimedes são poliedros convexos semi-regulares, ou seja, todos os seus lados são iguais, mas as faces são de dois ou mais tipos diferentes. Existem treze sólidos de Arquimedes.
Os sólidos de Arquimedes são chamados de semi-regulares porque todos os seus lados são iguais, mas as faces são de dois ou mais tipos diferentes.
- Cubo truncado: possui 14 faces (6 quadrados e 8 hexágonos), 36 arestas e 24 vértices.
- Octaedro truncado: possui 14 faces (8 triângulos e 6 quadrados), 36 arestas e 24 vértices.
- Icosaedro truncado: possui 32 faces (20 hexágonos e 12 decágonos), 90 arestas e 60 vértices.
- Dodecaedro truncado: possui 32 faces (12 decágonos e 20 hexágonos), 90 arestas e 60 vértices.
- Tetraedro truncado: possui 4 faces (4 hexágonos), 12 arestas e 4 vértices.
- Cubo truncado-rombico: possui 26 faces (12 quadrados e 14 hexágonos), 48 arestas e 24 vértices.
- Octaedro truncado-rombico: possui 26 faces (8 triângulos e 18 quadrados), 48 arestas e 24 vértices.
- Icosaedro truncado-rombico: possui 62 faces (20 triângulos e 42 quadrados), 120 arestas e 60 vértices.
- Dodecaedro truncado-rombico: possui 62 faces (12 pentágonos e 50 quadrados), 120 arestas e 60 vértices.
- Tetraedro truncado-rombico: possui 14 faces (4 hexágonos e 10 triângulos), 24 arestas e 12 vértices.
- Cubo truncado-rombico-triangular: possui 26 faces (8 triângulos, 12 quadrados e 6 octógonos), 48 arestas e 24 vértices.
- Octaedro truncado-rombico-triangular: possui 26 faces (6 quadrados, 8 hexágonos e 12 triângulos), 48 arestas e 24 vértices.
- Icosaedro truncado-rombico-triangular: possui 62 faces (20 triângulos, 30 quadrados e 12 decágonos), 120 arestas e 60 vértices.
Planificação de Poliedros: Exemplos De Planificação De Um Poliedro
A planificação de um poliedro é a representação plana de suas faces, como se o poliedro fosse “desdobrado” em um plano. Essa representação é útil para visualizar a estrutura do poliedro e entender como suas faces se conectam.
Planificação de Diferentes Tipos de Poliedros
A planificação de poliedros é um processo que pode ser aplicado a diferentes tipos de poliedros, como cubos, pirâmides, prismas e outros. Cada tipo de poliedro possui uma planificação específica, dependendo do número de faces, arestas e vértices. A planificação de um poliedro pode ser representada através de diagramas, onde cada face do poliedro é representada por um polígono plano, e as arestas são representadas por linhas que conectam os vértices dos polígonos.
Passos para Planificar um Poliedro
A planificação de um poliedro envolve os seguintes passos:
- Identificação das Faces:O primeiro passo é identificar todas as faces do poliedro. As faces são as superfícies planas que compõem o poliedro.
- Determinação do Número de Arestas e Vértices:É importante determinar o número de arestas e vértices do poliedro. As arestas são os segmentos de reta que conectam os vértices, e os vértices são os pontos onde as arestas se encontram.
- Organização das Faces:As faces do poliedro devem ser organizadas em um padrão plano, de modo que as arestas que se conectam em um poliedro também se conectem na planificação. As faces devem ser dispostas de forma que não haja sobreposição ou lacunas.
Tabela de Planificação de Poliedros
A tabela abaixo mostra os passos de planificação para diferentes tipos de poliedros:
| Tipo de Poliedro | Número de Faces | Número de Arestas | Número de Vértices |
|---|---|---|---|
| Cubo | 6 | 12 | 8 |
| Tetraedro | 4 | 6 | 4 |
| Pirâmide Quadrada | 5 | 8 | 5 |
| Prisma Triangular | 5 | 9 | 6 |
Aplicações da Planificação de Poliedros
A planificação de poliedros é uma ferramenta poderosa que encontra aplicações em diversas áreas, desde a arquitetura e engenharia até o design e as artes. A capacidade de desdobrar um objeto tridimensional em um plano bidimensional permite a visualização de suas faces e arestas, facilitando a análise, construção e produção de objetos complexos.
Aplicações na Arquitetura e Engenharia
A planificação de poliedros é fundamental na arquitetura e engenharia para o projeto e construção de estruturas complexas. Arquitetos e engenheiros usam a planificação para:
- Criar modelos de edifícios e estruturas, permitindo a visualização de seus elementos e a análise de sua estabilidade e funcionalidade.
- Desenvolver projetos de telhados, fachadas e outras superfícies complexas, garantindo a precisão e a eficiência da construção.
- Projetar sistemas de ventilação e iluminação, utilizando a geometria dos poliedros para otimizar o fluxo de ar e a entrada de luz.
Por exemplo, a planificação de um prisma retangular pode ser utilizada para construir um galpão com telhado inclinado, garantindo a drenagem da água da chuva.
Aplicações no Design e Artes
A planificação de poliedros também desempenha um papel importante no design e nas artes. Designers e artistas usam a planificação para:
- Criar embalagens inovadoras, explorando formas geométricas para otimizar o espaço e proteger o produto.
- Desenvolver objetos tridimensionais, como móveis, esculturas e peças de decoração, com formas complexas e originais.
- Criar obras de arte tridimensionais, utilizando a planificação de poliedros para construir esculturas, instalações e objetos de arte.
Por exemplo, a planificação de um cubo pode ser utilizada para criar uma caixa de presente com um design inovador, utilizando diferentes materiais e cores.
Aplicações na Educação
A planificação de poliedros é uma ferramenta pedagógica importante, auxiliando na compreensão de conceitos matemáticos como geometria espacial, área e volume. A construção de modelos tridimensionais a partir de planos bidimensionais permite a visualização e a manipulação de objetos geométricos, facilitando o aprendizado.
Aplicações em outras Áreas
A planificação de poliedros também encontra aplicações em outras áreas, como:
- Engenharia aeronáutica: no projeto de fuselagens e asas de aeronaves.
- Engenharia mecânica: no projeto de peças e componentes complexos.
- Ciências da computação: na criação de modelos 3D e na simulação de objetos tridimensionais.
A planificação de poliedros é uma ferramenta versátil que encontra aplicações em diversas áreas, contribuindo para a inovação e o desenvolvimento de soluções criativas e eficientes.
A planificação de poliedros oferece uma ferramenta poderosa para a compreensão e a criação de formas tridimensionais. Através do estudo dos diferentes tipos de poliedros e da aplicação de métodos de planificação, podemos explorar a relação entre geometria e design, abrindo caminho para novas possibilidades criativas e inovadoras em diversas áreas.
A capacidade de visualizar e manipular formas tridimensionais a partir de planos bidimensionais é essencial para a resolução de problemas práticos e para a criação de objetos inovadores.

