Lista De Exercícios Sobre Função Do 1º Grau – Mundo Educação: embarque numa jornada fascinante pelo universo das funções de primeiro grau! Prepare-se para desvendar os mistérios por trás dessas equações que modelam o mundo ao nosso redor, desde o cálculo de custos até a previsão de movimentos. Nesta exploração, vamos dominar as técnicas para resolver problemas, interpretar gráficos e aplicar esses conceitos em situações práticas, revelando a beleza e a utilidade da matemática no dia a dia.
Através de exemplos práticos e exercícios cuidadosamente selecionados, você irá construir uma compreensão sólida das funções do 1º grau. Aprenderá a identificar padrões, a resolver equações e inequações, e a visualizar graficamente as relações entre variáveis. Cada passo, cada desafio superado, será uma conquista que o aproximará de uma nova perspectiva sobre a matemática, mostrando-lhe a sua elegância e poder de explicação da realidade.
Tipos de Problemas Envolvendo Funções do 1º Grau: Lista De Exercícios Sobre Função Do 1º Grau – Mundo Educação
A jornada pelo universo das funções do 1º grau é repleta de desafios e descobertas fascinantes. Dominar essa área significa desvendar os segredos por trás de inúmeros fenômenos, desde o crescimento de uma população até a trajetória de um projétil. Prepare-se para embarcar nessa aventura matemática, explorando os diferentes tipos de problemas que nos aguardam.
Cálculo do Valor de y para um Dado Valor de x
Resolver problemas que pedem o cálculo de y para um determinado x é como decifrar um código secreto. A equação da reta, a chave para esse enigma, nos fornece a fórmula para encontrar a resposta. Basta substituir o valor conhecido de x na equação e realizar os cálculos necessários para obter o valor correspondente de y. Vejamos alguns exemplos:
| x | y | Equação | Solução |
|---|---|---|---|
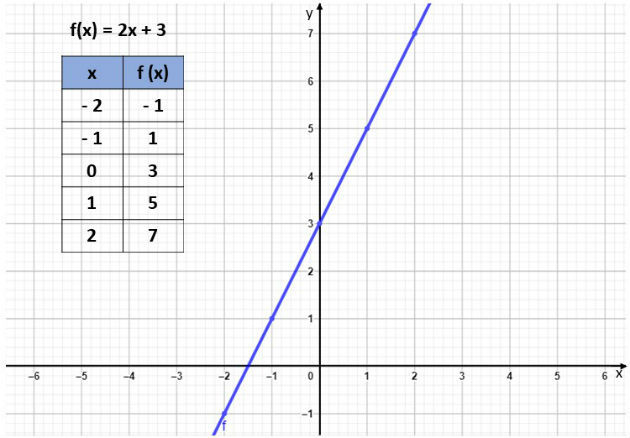
| 2 | 7 | y = 2x + 3 | y = 2(2) + 3 = 7 |
| -1 | 1 | y = x + 2 | y = (-1) + 2 = 1 |
| 0 | -1 | y = -x -1 | y = -(0) – 1 = -1 |
| 5 | 12 | y = 2x + 2 | y = 2(5) + 2 = 12 |
Determinação da Equação da Reta a Partir de Dois Pontos Dados, Lista De Exercícios Sobre Função Do 1º Grau – Mundo Educação
Imagine ter dois pontos perdidos em um mapa. Para traçar a reta que os une, precisamos encontrar sua equação. Esse processo envolve a determinação do coeficiente angular (m) e o uso da equação da reta na forma ponto-reta.
- Encontre o coeficiente angular (m): O coeficiente angular representa a inclinação da reta e é calculado pela fórmula:
m = (y₂
- y₁) / (x₂
- x₁)
onde (x₁, y₁) e (x₂, y₂) são as coordenadas dos dois pontos.
- Utilize a equação ponto-reta: Com o coeficiente angular (m) e as coordenadas de um dos pontos (x₁, y₁), podemos utilizar a equação ponto-reta para determinar a equação da reta:
y – y₁ = m(x – x₁)
- Simplifique a equação: Após a substituição dos valores, simplifique a equação para a forma y = mx + b, onde b é o coeficiente linear (interseção com o eixo y).
Interpretação Gráfica de Funções do 1º Grau

A representação gráfica de uma função do 1º grau nos permite visualizar sua trajetória e extrair informações importantes. O gráfico é uma reta, onde o coeficiente angular (m) determina sua inclinação e o coeficiente linear (b) indica o ponto de interseção com o eixo y. A raiz da função (ponto onde a reta cruza o eixo x) é obtida fazendo y = 0 e resolvendo a equação para x.Para criar um gráfico representativo, siga estes passos:
- Determine dois pontos da reta: Escolha dois valores de x e calcule os correspondentes valores de y utilizando a equação da função.
- Marque os pontos no plano cartesiano: Localize os pontos (x, y) no plano cartesiano, onde o eixo x é horizontal e o eixo y é vertical.
- Trace a reta: Una os dois pontos com uma linha reta, estendendo-a para além dos pontos marcados. Esta reta representa o gráfico da função do 1º grau.
A inclinação da reta visualmente indica o valor do coeficiente angular: uma reta ascendente possui coeficiente angular positivo, enquanto uma reta descendente possui coeficiente angular negativo. A interseção com o eixo y indica o valor do coeficiente linear.
Aplicações Práticas de Funções do 1º Grau
A beleza da matemática reside em sua capacidade de descrever o mundo ao nosso redor. As funções do 1º grau, com sua simplicidade e elegância, revelam-se ferramentas poderosas para modelar situações cotidianas, desde o cálculo de custos de uma viagem até a previsão do crescimento de uma população. Sua aplicabilidade transcende os muros da sala de aula, encontrando espaço em diversas áreas do conhecimento e da vida prática.
Nesta seção, exploraremos algumas dessas aplicações, desvendando a magia por trás de sua utilidade.As funções do 1º grau, representadas pela equação geral y = mx + b, onde ‘m’ representa a inclinação e ‘b’ o ponto de interseção com o eixo y, permitem-nos estabelecer relações lineares entre duas variáveis. Essa relação linear é a chave para a modelagem de diversos fenômenos.
A constância da taxa de variação (m) é o elemento crucial que permite a precisão dessas previsões em um determinado intervalo.
Exemplos de Situações Cotidianas Modeladas por Funções do 1º Grau
Observemos como a simplicidade das funções do 1º grau nos permite entender e prever comportamentos complexos.
Exemplo 1: Cálculo de Custos. Uma empresa de táxi cobra R$ 5,00 de bandeirada e R$ 2,00 por quilômetro rodado. Podemos modelar o custo total (C) em função da distância percorrida (d) pela equação: C = 2d + 5. Se um cliente percorrer 10 km, o custo será C = 2(10) + 5 = R$ 25,00.
Exemplo 2: Velocidade e Distância. Um carro viaja a uma velocidade constante de 80 km/h. A distância percorrida (d) em função do tempo (t) pode ser representada por: d = 80t. Após 3 horas de viagem, o carro terá percorrido d = 80(3) = 240 km.
Exemplo 3: Preço de um Produto com Desconto. Uma loja oferece um desconto de 10% em todos os produtos. Se o preço original de um produto é ‘x’, o preço com desconto (y) será dado por: y = x – 0.1x = 0.9x. Se um produto custa R$ 100,00, o preço com desconto será y = 0.9(100) = R$ 90,00.
Comparação entre Aplicações de Funções do 1º Grau
Comparando os exemplos de cálculo de custos e velocidade e distância, notamos similaridades e diferenças importantes na modelagem matemática. Ambas as situações utilizam uma relação linear direta entre duas variáveis, permitindo a representação gráfica como uma reta. A similaridade reside na constância da taxa de variação: R$ 2,00 por quilômetro no caso do táxi e 80 km/h no caso do carro.
A diferença reside na interpretação das variáveis: no primeiro caso, temos custo e distância, enquanto no segundo, temos distância e tempo. A inclinação da reta representa a taxa de variação em cada caso, refletindo o custo por quilômetro ou a velocidade constante.
Problemas que Demonstram a Utilidade das Funções do 1º Grau em Diferentes Áreas

As funções do 1º grau são ferramentas essenciais em diversas áreas do conhecimento.A seguir, uma lista de problemas que demonstram sua aplicabilidade:
Problema 1 (Física): Um corpo em queda livre tem sua velocidade (v) em função do tempo (t) dada por v = gt, onde g é a aceleração da gravidade. Determine a velocidade após 5 segundos considerando g = 9.8 m/s².
Problema 2 (Economia): O custo de produção (C) de um certo produto é dado por C = 10x + 500, onde x é a quantidade produzida. Determine o custo de produção de 100 unidades.
Problema 3 (Geografia): A população de uma cidade cresce linearmente a uma taxa de 200 habitantes por ano. Se a população atual é de 10.000 habitantes, qual será a população daqui a 5 anos?
Resolução de Equações e Inequações do 1º Grau

A jornada pela álgebra nos leva a um território fascinante: a resolução de equações e inequações do primeiro grau. Dominar essas ferramentas é como ganhar uma chave-mestra para desvendar os enigmas matemáticos que permeiam diversas áreas do conhecimento, desde a física e a engenharia até a economia e a programação. Prepare-se para embarcar nessa aventura!
Equações e inequações do primeiro grau são expressões algébricas que representam relações de igualdade ou desigualdade entre variáveis e constantes. A habilidade de resolvê-las é fundamental para modelar e solucionar problemas do mundo real, permitindo-nos traduzir situações complexas em linguagem matemática e encontrar soluções precisas e eficientes.
Resolução de Equações do 1º Grau com uma Incógnita
A resolução de uma equação do 1º grau consiste em encontrar o valor da incógnita (geralmente representada pela letra x) que torna a igualdade verdadeira. Para isso, aplicamos propriedades da igualdade, buscando isolar a incógnita em um dos membros da equação. O objetivo final é encontrar o valor de ‘x’ que satisfaz a equação.
A seguir, apresentamos alguns exemplos, detalhando cada passo para uma compreensão completa do processo. Observe a organização dos dados na tabela para facilitar a sua aprendizagem.
| Equação | Passos da Resolução | Solução | Verificação |
|---|---|---|---|
| 2x + 5 = 9 |
1. Subtrair 5 de ambos os lados 2x = 4 2. Dividir ambos os lados por 2 x = 2 |
x = 2 | 2(2) + 5 = 9 4 + 5 = 9 9 = 9 (Verdadeiro) |
| 3x – 7 = 8 |
1. Adicionar 7 a ambos os lados 3x = 15 2. Dividir ambos os lados por 3 x = 5 |
x = 5 | 3(5)
|
| -x + 4 = 1 |
1. Subtrair 4 de ambos os lados -x = -3 2. Multiplicar ambos os lados por -1 x = 3 |
x = 3 | -(3) + 4 = 1 -3 + 4 = 1 1 = 1 (Verdadeiro) |
| 5x/2 – 3 = 7 |
1. Adicionar 3 a ambos os lados 5x/2 = 10 2. Multiplicar ambos os lados por 2 5x = 20 3. Dividir ambos os lados por 5 x = 4 |
x = 4 | 5(4)/2 – 3 = 7 10 – 3 = 7 7 = 7 (Verdadeiro) |
Resolução de Inequações do 1º Grau
As inequações do 1º grau, ao contrário das equações, expressam desigualdades. A resolução segue princípios semelhantes às equações, mas com uma peculiaridade: ao multiplicar ou dividir por um número negativo, inverte-se o sentido da desigualdade. A solução de uma inequação é um conjunto de valores que satisfazem a desigualdade, frequentemente representado graficamente na reta numérica.
Vejamos alguns exemplos para ilustrar a resolução e a representação gráfica:
Exemplo 1: 2x + 3 > 7
Resolução: 2x > 4 => x > 2
Representação gráfica: Uma reta numérica com um círculo aberto em 2 e uma seta apontando para a direita, indicando todos os números maiores que 2.
Exemplo 2: -x + 5 ≤ 2
Resolução: -x ≤ -3 => x ≥ 3
Representação gráfica: Uma reta numérica com um círculo fechado em 3 e uma seta apontando para a direita, indicando 3 e todos os números maiores que 3.
Exemplo 3: 3x – 1 < 8
Resolução: 3x < 9 => x < 3
Representação gráfica: Uma reta numérica com um círculo aberto em 3 e uma seta apontando para a esquerda, indicando todos os números menores que 3.
Resolução de Sistemas de Equações do 1º Grau com Duas Incógnitas
Sistemas de equações do 1º grau envolvem duas ou mais equações com duas ou mais incógnitas. Para resolvê-los, buscamos encontrar os valores das incógnitas que satisfazem simultaneamente todas as equações. Dois métodos comuns são o método da substituição e o método da adição.
Vamos explorar o método da substituição e o método da adição com exemplos práticos.
Método da Substituição:
- Isolar uma variável em uma das equações.
- Substituir a expressão encontrada no passo 1 na outra equação.
- Resolver a equação resultante para encontrar o valor de uma variável.
- Substituir o valor encontrado no passo 3 em qualquer uma das equações originais para encontrar o valor da outra variável.
Método da Adição:
- Multiplicar as equações por constantes apropriadas para que os coeficientes de uma das variáveis sejam opostos.
- Somar as equações resultantes para eliminar a variável com coeficientes opostos.
- Resolver a equação resultante para encontrar o valor de uma variável.
- Substituir o valor encontrado no passo 3 em qualquer uma das equações originais para encontrar o valor da outra variável.

